<html>
<head>
<meta http-equiv="Content-Type" content="text/html; charset=US-ASCII">
<title>Overview</title>
<link rel="stylesheet" href="../math.css" type="text/css">
<meta name="generator" content="DocBook XSL Stylesheets V1.79.1">
<link rel="home" href="../index.html" title="Math Toolkit 2.5.1">
<link rel="up" href="../octonions.html" title="Chapter 10. Octonions">
<link rel="prev" href="../octonions.html" title="Chapter 10. Octonions">
<link rel="next" href="oct_header.html" title="Header File">
</head>
<body bgcolor="white" text="black" link="#0000FF" vlink="#840084" alink="#0000FF">
<table cellpadding="2" width="100%"><tr>
<td valign="top"><img alt="Boost C++ Libraries" width="277" height="86" src="../../../../../boost.png"></td>
<td align="center"><a href="../../../../../index.html">Home</a></td>
<td align="center"><a href="../../../../../libs/libraries.htm">Libraries</a></td>
<td align="center"><a href="http://www.boost.org/users/people.html">People</a></td>
<td align="center"><a href="http://www.boost.org/users/faq.html">FAQ</a></td>
<td align="center"><a href="../../../../../more/index.htm">More</a></td>
</tr></table>
<hr>
<div class="spirit-nav">
<a accesskey="p" href="../octonions.html"><img src="../../../../../doc/src/images/prev.png" alt="Prev"></a><a accesskey="u" href="../octonions.html"><img src="../../../../../doc/src/images/up.png" alt="Up"></a><a accesskey="h" href="../index.html"><img src="../../../../../doc/src/images/home.png" alt="Home"></a><a accesskey="n" href="oct_header.html"><img src="../../../../../doc/src/images/next.png" alt="Next"></a>
</div>
<div class="section">
<div class="titlepage"><div><div><h2 class="title" style="clear: both">
<a name="math_toolkit.oct_overview"></a><a class="link" href="oct_overview.html" title="Overview">Overview</a>
</h2></div></div></div>
<p>
Octonions, like <a class="link" href="../quaternions.html" title="Chapter 9. Quaternions">quaternions</a>, are a relative
of complex numbers.
</p>
<p>
Octonions see some use in theoretical physics.
</p>
<p>
In practical terms, an octonion is simply an octuple of real numbers (α,β,γ,δ,ε,ζ,η,θ), which
we can write in the form <span class="emphasis"><em><code class="literal">o = α + βi + γj + δk + εe' + ζi' + ηj' + θk'</code></em></span>, where
<span class="emphasis"><em><code class="literal">i</code></em></span>, <span class="emphasis"><em><code class="literal">j</code></em></span>
and <span class="emphasis"><em><code class="literal">k</code></em></span> are the same objects as for quaternions,
and <span class="emphasis"><em><code class="literal">e'</code></em></span>, <span class="emphasis"><em><code class="literal">i'</code></em></span>,
<span class="emphasis"><em><code class="literal">j'</code></em></span> and <span class="emphasis"><em><code class="literal">k'</code></em></span>
are distinct objects which play essentially the same kind of role as <span class="emphasis"><em><code class="literal">i</code></em></span>
(or <span class="emphasis"><em><code class="literal">j</code></em></span> or <span class="emphasis"><em><code class="literal">k</code></em></span>).
</p>
<p>
Addition and a multiplication is defined on the set of octonions, which generalize
their quaternionic counterparts. The main novelty this time is that <span class="bold"><strong>the multiplication is not only not commutative, is now not even
associative</strong></span> (i.e. there are octonions <span class="emphasis"><em><code class="literal">x</code></em></span>,
<span class="emphasis"><em><code class="literal">y</code></em></span> and <span class="emphasis"><em><code class="literal">z</code></em></span>
such that <span class="emphasis"><em><code class="literal">x(yz) ≠ (xy)z</code></em></span>). A way of remembering
things is by using the following multiplication table:
</p>
<p>
<span class="inlinemediaobject"><img src="../../octonion/graphics/octonion_blurb17.jpeg"></span>
</p>
<p>
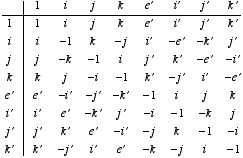
Octonions (and their kin) are described in far more details in this other
<a href="../../quaternion/TQE.pdf" target="_top">document</a> (with <a href="../../quaternion/TQE_EA.pdf" target="_top">errata
and addenda</a>).
</p>
<p>
Some traditional constructs, such as the exponential, carry over without too
much change into the realms of octonions, but other, such as taking a square
root, do not (the fact that the exponential has a closed form is a result of
the author, but the fact that the exponential exists at all for octonions is
known since quite a long time ago).
</p>
</div>
<table xmlns:rev="http://www.cs.rpi.edu/~gregod/boost/tools/doc/revision" width="100%"><tr>
<td align="left"></td>
<td align="right"><div class="copyright-footer">Copyright © 2006-2010, 2012-2014 Nikhar Agrawal,
Anton Bikineev, Paul A. Bristow, Marco Guazzone, Christopher Kormanyos, Hubert
Holin, Bruno Lalande, John Maddock, Jeremy Murphy, Johan Råde, Gautam Sewani,
Benjamin Sobotta, Thijs van den Berg, Daryle Walker and Xiaogang Zhang<p>
Distributed under the Boost Software License, Version 1.0. (See accompanying
file LICENSE_1_0.txt or copy at <a href="http://www.boost.org/LICENSE_1_0.txt" target="_top">http://www.boost.org/LICENSE_1_0.txt</a>)
</p>
</div></td>
</tr></table>
<hr>
<div class="spirit-nav">
<a accesskey="p" href="../octonions.html"><img src="../../../../../doc/src/images/prev.png" alt="Prev"></a><a accesskey="u" href="../octonions.html"><img src="../../../../../doc/src/images/up.png" alt="Up"></a><a accesskey="h" href="../index.html"><img src="../../../../../doc/src/images/home.png" alt="Home"></a><a accesskey="n" href="oct_header.html"><img src="../../../../../doc/src/images/next.png" alt="Next"></a>
</div>
</body>
</html>